Question: You are given a 2D array of characters and a character pattern. WAP to find if pattern is present in 2D array. Pattern can be in any way (all 8 neighbors to be considered) but you can’t use same character twice while matching. Return 1 if match is found, 0 if not.
Example: Find “microsoft” in below matrix.

We can see the read color character, which form “Microsoft” in above 2D array.
Answer: I was asked this question in a Microsoft interview almost a year ago. A reader asked me to post the solution for this.
Manually finding the solution of this problem is relatively intuitive, we just need to describe an algorithm for it. Ironically, describing the algorithm is not the easy part.
How do we do it manually? First we match the first element; if it matched we matched the 2nd element in the 8 neighbors of first match; do this process recursively; when last character of input pattern matches, return true.
During above process, you take care not to use any cell in 2D array twice. For this purpose, you mark every visited cell with some sign. If your pattern matching fails at some place, you start matching from the beginning (of pattern) in remaining cells. While returning, you unmark visited cells.
Lets convert above intuitive method in algorithm. Since we are doing similar checks every time for pattern matching, a recursive solution is what we need here.
In recursive solution, we need to check if the substring passed is matched in the given matrix or not. The condition is not to use the already used cell. For finding already used cell, we need to have another 2D array to the function (or we can use an unused bit in input array itself.) Also, we need the current position of input matrix, from where we need to start. Since we need to pass a lot more information than actually given, we should be having a wrapper function to initialize that extra information to be passed.
Algorithm:
If you are past the last character in pattern
Return true
If you got an used cell again
Return falseIf you got past the 2D matrix
Return false
If searching for first element and cell doesn’t match
findmatch with next cell in row-first order (or column first order)
otherwise if character matches
mark this cell as used
res = findmatch with next position of pattern in 8 neighbors
mark this cell as unused
Return res
Otherwise
Return false
Code:
#define MAX 100
//level: index till which pattern is matched
//x, y: current position in 2D array
bool findmatch(char mat[MAX][MAX], char *pat, int x, int y, int nrow, int ncol, int level)
{
if (level == strlen(pat)) //pattern matched
return true;
if (x<0 || y<0 || x>=nrow || y>=ncol)
return false;
if (mat[x][y] == pat[level])
{
// printf("{%d, %d}\n",x,y);
bool res;
//marking this cell as used
char temp = mat[x][y];
mat[x][y] = '#';
//finding subpattern in 8 neighbours
res = findmatch(mat, pat, x-1, y, nrow, ncol, level+1) ||
findmatch(mat, pat, x+1, y, nrow, ncol, level+1) ||
findmatch(mat, pat, x, y-1, nrow, ncol, level+1) ||
findmatch(mat, pat, x, y+1, nrow, ncol, level+1) ||
findmatch(mat, pat, x+1, y+1, nrow, ncol, level+1) ||
findmatch(mat, pat, x+1, y-1, nrow, ncol, level+1) ||
findmatch(mat, pat, x-1, y+1, nrow, ncol, level+1) ||
findmatch(mat, pat, x-1, y-1, nrow, ncol, level+1);
//marking this cell as unused
mat[x][y] = temp;
return res;
}
else
return false;
}
bool findmatch_wrapper(char mat[MAX][MAX], char *pat, int nrow, int ncol)
{
// if total characters in matrix is less then pattern lenghth
if (strlen(pat) > nrow*ncol)
return false;
for (int i=0; i<nrow; i++)
for (int j=0; j<ncol; j++){
if (mat[i][j] == pat[0])
if(findmatch(mat, pat, i, j, nrow, ncol, 0))
return true;
}
return false;
}
Please note the use of OR operator while calculating res. This confirms me that I don’t evaluate next condition as soon as one of the conditions evaluates to true.
Complexity:
Best case complexity is obviously O(1), if pattern is NULL.
Worst case: What will be worst case for this problem. The matrix (lets say N*N) is filled with ‘A’ in all the cells and pattern is “AAAA…….AAAAB” of length N^2. Then it will match with every cell, search in 8 neighbors recursively and fails at last element every time.
I'm leaving it to readers to find the complexity of this approach.
Subscribe - To get an automatic feed of all future posts subscribe here, or to receive them via email go here and enter your email address in the box. You can also like us on facebook and follow me on Twitter @akashag1001.
 Lets assume that person 1 speaks truth then all including him should be liar. It means he doesn’t speak truth.
Lets assume that person 1 speaks truth then all including him should be liar. It means he doesn’t speak truth.
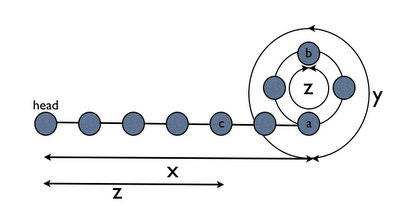 In above figure, we see that loop starts at node (a) after length x and loop length is z. So the total length of link list is (x+z). Also as we saw in
In above figure, we see that loop starts at node (a) after length x and loop length is z. So the total length of link list is (x+z). Also as we saw in 
 A 1000m race also takes place on a circular track but athletes have to make multiple rounds of the same track (we can say this track as a loop in the list.) What if there is no finish line, an athlete has to run forever (because of no null pointer in the end.) Now if athlete X runs faster than athlete Y, X is bound to leave Y behind at some point. In the process, there will be a time when X and Y are at same place.
A 1000m race also takes place on a circular track but athletes have to make multiple rounds of the same track (we can say this track as a loop in the list.) What if there is no finish line, an athlete has to run forever (because of no null pointer in the end.) Now if athlete X runs faster than athlete Y, X is bound to leave Y behind at some point. In the process, there will be a time when X and Y are at same place. Answer: Please notice that we can put tiles either vertically or horizontally. For putting vertical tiles, we need a gap of at least 2 X 2. For putting horizontal tiles, we need a gap of 2 X 1. Number of arrangements will be the same as the arrangements, we can make with gaps of 1 and 2 (order dependent). In this manner, this problem reduces to find the number of ways to partition N using the numbers 1 and 2 with order considered relevant.
Answer: Please notice that we can put tiles either vertically or horizontally. For putting vertical tiles, we need a gap of at least 2 X 2. For putting horizontal tiles, we need a gap of 2 X 1. Number of arrangements will be the same as the arrangements, we can make with gaps of 1 and 2 (order dependent). In this manner, this problem reduces to find the number of ways to partition N using the numbers 1 and 2 with order considered relevant.

 Answer: We should have one fact in mind that merging node is found by comparing the address (not value) of the nodes. Since we have 2 different lists, one way is to have 2 for loops and compare addresses of all the possible nodes. This solution is O(mn) where 'm' and 'n' are lengths of given lists.
Answer: We should have one fact in mind that merging node is found by comparing the address (not value) of the nodes. Since we have 2 different lists, one way is to have 2 for loops and compare addresses of all the possible nodes. This solution is O(mn) where 'm' and 'n' are lengths of given lists.