In last post, we found how to detect if there is a loop in singly link list or not. Now we will see how to detect where the loop starts.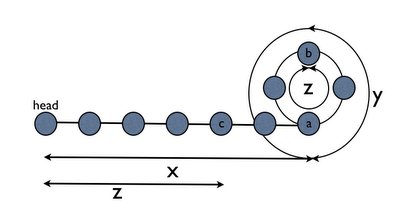
In above figure, we see that loop starts at node (a) after length x and loop length is z. So the total length of link list is (x+z). Also as we saw in last post that slow and fast iterator will meet at some node (b).
Please note if we move a pointer (one node per iteration) from (b) and keep count of nodes until we visit (b) again, we will be able to calculate z.
After finding z, start an iterator itr1 form head and move it z nodes from head at (c). Take another iterator itr2 and start it from head. Now if you move itr1 and itr2 in parallel one node at a time, they will meet first at start of the loop (a).
Explanation is based on following invariance:
"In a circle if we start from some point and move the distance equal to circumference along circle periphery, we will be at the same point again."
Both the iterators are meeting at (a) coz itr1 is z nodes ahead from itr2. Once itr1 is at (a), itr2 is z nodes behind (a). After z iterations, itr2 will reach (a) and itr1 also reaches (a) because of above invariant.
This solution has been suggested by Saket in comments to last post. Great solution Saket!
Subscribe - To get an automatic feed of all future posts subscribe here, or to receive them via email go here and enter your email address in the box. You can also like us on facebook and follow me on Twitter @akashag1001.
Another solution where we don't need to find the length of loop (z) is :
The fast and slow iterator meets at node b which is at a distance of y from node a. We can easily prove that (x + y) = nz where n is a natural number. (using speed, distance formula)
Now start two iterators of same speed of 1 from node b and from the head node. The first node which they will meet is the node a which is also the start of the linked list.
@Saurabh: Can you please explain with an example. What if x=2, y=2 and z=10.
@Akash,
you can only choose x and z, y will be the result. So, saying that x =2, y =2 and z = 10 is not correct.
Lets take x = 2 and z = 10. Now, if slow and fast pointer will move, they will meet at a point where y = 8. (we can calculate it on paper). so, when we will start two pointers, they will meet at the start of loop.
Let me explain it in terms of maths.
vf = speed of fast iterator
vs = speed of slow iterator
df = distance moved by fast iterator
ds = distance moved by slow iterator
now, speed = distance / time
so, vf = df/t and vs = ds/t (time is same when they meet)
and we know vf = 2vs, so df = 2 ds.
Now, df = x + nz + y (n is some natural number)
and ds = x + y
So, (x + y) = nz
this above statement means that x distance is equal to nz - y. When an iterator will start from head and move x distance forward, the another iterator from y location (with single step speed) will cover (nz - y) distance. If we analyse then (nz -y) is nothing but the start of the loop.
I hope this clears the point.
@Saurabh: Awesome explanation! It works!
If i start with 2 pointers from head ptr1 and ptr2 and ptr1 is increemented by one whereas ptr2 is increemented by 2 then both meet at 'a' node. From this point if I apply sourabh's solution (i.e. pull onr ptr back to head and iterate both the pointers by one) then they'll never meet.
Nice explanation. Another good explanation with equations is at http://kamaljeet-verma.blogspot.com
This is an excellent website. This is my first visit to this blog, and I think it's amazing. The most important thing is that this blog's information is written in a clear and understandable manner.Custom Web Design and Development
Enjoyed reading the article above , really explains everything in detail,the article is very interesting and effective.Thank you and good luck for the upcoming articles.
Custom Web Development
Thank you very much for taking the time to share this important information with us. This is incredible.
SEO Services NYC