Question: There is an N x N matrix with the property that each entry in the matrix is the smallest non-negative number, which does not appear either above the entry or to its left. Write a method to find the entry in a particular row and column.

For example, for N=8, we might have the matrix: 

0    1    2    3    4    5    6    7
1    0    3    2    5    4    7    6
2    3    0    1    6    7    4    5
3    2    1    0    7    6    5    4
4    5    6    7    0    1    2    3
5    4    7    6    1    0    3    2
6    7    4    5    2    3    0    1
7    6    5    4    3    2    1    0


Answer: From the question statement, it is clear that the top left corner starts things off with 0 and the top row and the leftmost column are each completed with the positive integers 1,2,3,..., in order.

Secondly, if every time we fill another cell, we use the smallest non-negative integers that have not so far appeared in the same column and the same row, then it is impossible to get a repeated integer in either the same column or the same row. Square matrix of order n, in which every symbol occurs exactly once in each row and column of the array, is called latin square. So we can say that above matrix is a latin square in different setting.

Lets see if we can find some pattern in the sequence. If we write the matrix in binary number system an 8*8 matrix will look like below matrix:


If we split this 2n square matrix in 4 parts of size 2n-1 and call them as Mtl, Mtr, Mbr, Mbl (top-left, top-right, bottom-left, bottom-right respectively), each of these sub-matrixes is a latin square in itself.

If we took the highest power of 2 from these values, we can also write this matrix as


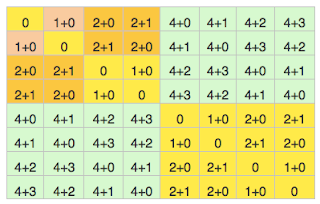
Lets see how this works. First, fill the corner square of size 1x1 with the number 0. On the next step, we get a square of size 2x2. The latter consists of four squares (Mtl, Mtr, Mbr, Mbl ) equal in size to the square on the previous step. Mtl is the square from the previous step. Copy it into three other squares, and lastly add 1 (2o) to every element of Mtr and Mbl.

Now at every step for generating a square matrix of size 2n+1, we can expand the matrix by assuming that a corner square of size 2n (Mtl) has been filled. Copy it into adjacent squares Mtr, Mbr and Mbl and add 2n to every element of Mtr and Mbl. Final relationship will be like shown below:


How can we prove that resultant matrix has the required property?

Lets prove it my using mathematical induction. We have seen that M0 adhere to the property. Now assume that MN-1 follow the property, lets show that MN also follow the same:

Since we assumed that MN-1 (i.e. Mtl for MN) follows theis rule and entries of Mtr are formed by adding 2N-1 to Mtl. So Mtr is a latin square in itself. Also since elements from 0 to (2N-1 - 1) have already been used in Mtl, candidates for Mtr are only values greater than or equal to 2N-1. So we can say that Mtr adheres to the given rule. Similar argument can be given for Mbl.

For Mbr, we see that value for 0..(2N-1 -1) are not used in these row and column yet, We can use them and we used Mtl as it is. Hence we prove that MN the given conditions.

Now we can calculate value at any row and column in O(logN) time as on every step we can reduce the matrix size by half.

Can we do it in constant time?

Assume that rows and columns starting with 0 as in C/C++. Let M(m,n) denotes the number that appears in the (m, n) cell. Since we can denote any number with addition of power of 2, lets say

m = 2a + 2b + 2c + ... where a > b > c...
n = 2x + 2y + 2z + ... where x > y > z...

If a = x: then (m, n) lies in the Mbr square of the smallest square MN that contains (m, n). By dropping 2a from m and 2x from n, the point is moved into MN-1. So we don’t bother about ath and xth bit from m and n respectively.


If a < x: then (m, n) lies in the Mtr square of the smallest square MN that contains (m, n). As we saw earlier, we can move it into MN-1 by dropping 2a from m and add 2a to result. So we don’t bother about ath bit if it diffres.

If a > x: then (m, n) lies in the Mbl square of the smallest square MN that contains (m, n). As we saw earlier, we can move it into MN-1 by dropping 2x from n and add 2x to result. So we don’t bother about xth bit if it differs.

The process will continue while either m or n are not zero. Every time one of them has a binary bit which is 0 in the other, this bit is removed from the number but added to result. So we see that whenever any bit of m and n differs, we need to add it to result and just drop it if it’s same. In Boolean mathematics, XOR operator does the same. At the end of the day, m = n = 0 whereas result contains (m XOR n) of the original m and n. So finally
M(m,n) = m^n
Hence, we see that we can calculate the entry in a particular row and column in constant time and space.


Subscribe - To get an automatic feed of all future posts subscribe here, or to receive them via email go here and enter your email address in the box. You can also like us on facebook and follow me on Twitter @akashag1001.