Question: Take a binary tree and rearrange left and right pointers to make a circular doubly linked list.
Or
Convert a BST to a sorted circular doubly-linked list in-place.You are supposed to play with pointers only. Assume left and right pointers of tree as previous and next pointers of doubly-linked list.
Answer: This is one of the most asked problems in programming interviews. Microsoft asks this question very frequently, I was asked the same when I rejected SDE-2 offer from Microsoft a few months ago. You can also find this problem at Stanford CS education library page as The Great Tree List Recursion Problem.
Below is original tree, which we have to convert in a circular doubly linked list.

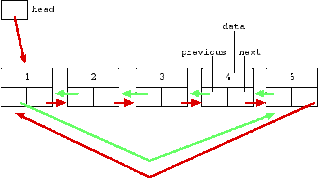
And below is the original tree converted to circular doubly linked list with "next" and "previous" list arrows added.
Above drawing shows the all of the problem state -- the original tree is drawn with plain black lines and the desired next/previous pointers are added in as arrows. Notice that starting with the head pointer.
Looking at the last figure, you might have already started thinking about in-order traversal. If not then please notice that in final linked list (shown below), all the nodes left to a node were actually the nodes from left-sub-tree in original tree. Similarly, all the nodes right to a node were actually the nodes from right-sub-tree in original tree. This is similar to in-order traversal of tree:
- process left sub tree
- process current node
- process right sub tree.
As we traverse the tree in-order, we can modify a node’s left pointer to point to its predecessor. We also have to modify the predecessor’s right pointer to point to the current node to maintain the doubly linked list behavior.
In this manner, we will be creating a list but that won’t be circular. We can solve this problem by creating a circular doubly linked list at every step in place of creating only doubly linked list. For this, we need to update the current node’s right pointer to point back to the head and the head’s left pointer to point to current node in each recursive call. As the recursion ends, the list’s head and tail would be automatically updated with the correct pointers.
Code:
struct node {
int data;
struct node* left;
struct node* right;
};
typedef struct node* Node;
//root: Current tree node
//prev: this pointer should have the address of in-order predecessor of root
//head: this denoted head of final link list
void treeToDoublyList(Node root, Node & prev, Node & head)
{
if (!root) return;
treeToDoublyList(root->left, prev, head);
// current node's left points to previous node
root->left = prev;
if (prev)
prev->right = root; // previous node's right points to current node
else
head = root; // if previous is NULL that current node is head
Node right = root->right; //Saving right node
//Now we need to make list created till now as circular
head->left = root;
root->right = head;
//For right-subtree/parent, current node is in-order predecessor
prev = root;
treeToDoublyList(right, prev, head);
}
//Wrapper function
Node treeToDoublyList(Node root)
{
Node prev = NULL;
Node head = NULL;
treeToDoublyList(root, prev, head);
return head;
}
Complexity: As this is nothing but in-order traversal with some extra steps at every node, we are traversing each node just once. Hence time complexity is O(n).
Credits: All the images are copied from Stanford CS library page.
Subscribe - To get an automatic feed of all future posts subscribe here, or to receive them via email go here and enter your email address in the box. You can also like us on facebook and follow me on Twitter @akashag1001.

Superb friend...
Best explanation on this topic!!
Subtraction Trading (Add Ten, Add Ten Method) | Student Tutorial Subtraction 2016 https://www.youtube.com/watch?v=bkmad_Mp_jY !
Thank you very much for drawing my notice to this. Your blog is jam-packed with useful facts. Until I read that, I would have no idea. I'll come back for more fantastic material. Best wishes, and good luck.
-Custom Web Design
This is a fantastic article. Your essay is quite simple to comprehend. Thank you for sharing this informative information with us.Web Design Customization
You did an excellent job! This is a very useful article. This appeals to me much. It is quite beneficial to my research. It clearly demonstrates your enthusiasm for the subject. I'm hoping you'll provide more details regarding the software. Please continue to share.
Software Testing Services