Question: Find the maximum rectangle (in terms of area) under a histogram in linear time. I mean the area of largest rectangle that fits entirely in the Histogram.

(Please refer figures before code section for clarity. If I include bar i completely, those figure will tell how much maximum area rectangle I can get.)

Answer: A straightforward answer is to go for each bar in the histogram and find the maximum possible area in histogram for it. Finally find the maximum of these values. This will require O(n^2) time but this will be huge if we have a big histogram with thousands of bars. So we need to have an algorithm of O(n*logn) or O(n).

Lets see if we can find one such solution:

There are a few invariants, we can use for this problem:
  1. If we include bar i, maximum possible height of rectangle including that bar will be h(i), height of that bar.
  2. If we include bar i, maximum possible width of rectangle including that bar will be L+R+1, where:
  • L is number of adjacent bars to the left of ith bar and height greater than or equal to h(i).
  • R is number of adjacent bars to the right of ith bar and height greater than or equal to h(i).
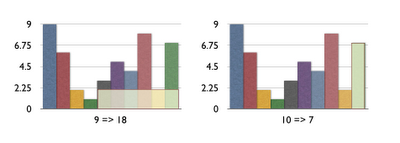
For the figure in question, if we include bar i, we will have max area as given in below pictures.

Now our task remains as follows:
1) Get Li
2) Get Ri
3) Get area of rectangle for bar i: A(i) = h(i) * (Li+Ri+1)
4) Find max value of A(i)


How to get Li:
Li is the number of adjacent bars to the left of ith bar and height greater than h(i). How can we calculate this?

One solution is to for each I, traverse through i to 0 until you get a bar of height less than h(i). This will be an O(n^2) solution to find all the Li.

But we can have a better solution, which works in less than O(n^2). Lets see an example; in example figure, what is the farthest bar greater than or equal to h(9) (h(9) =2 in our case). Here we are seeing that 4th bar is just short of h(9), so we can move left till 5th bar. So we don’t need to compare with 3rd, 2nd and 1st bar in this case.

Similarly, if I want to put a new value in the stack, which points we should compare h(i) to find L? : 10th, 9th and 4 th. Coz if we can include 9th bar, we can certainly include 8th, 7th, 6th and 5th bar as they have height greater than h(9).

Now if I use a stack and put only those bars in stack, which are possible candidates. And pop those values until I get a bar with height less than h(i). Finally Li = (i – TOP-of-stack).


Complexity: In first impression, this solution seems to be having O(n^2) complexity. But if we look carefully, we can just put at the max N bars in stack at any point in time. And we are not pushing any bar twice. So we can pop at most N bar while calculating Li for complete histogram. So work time complexity is O(n+n) = O(2n) = O(n)

How to get Ri:
Similarly as we found Li. Just start from the end in place of beginning.

Code:

int largestArea(int arr[], int len)
{
int area[len]; //initialize it to 0
int n, i, t;
stack<int> St;  //include stack for using this #include<stack>
bool done;

for (i=0; i<len; i++)
{
while (!St.empty())
{
   if(arr[i] <= arr[St.top()])
   {
       St.pop();
   }
   else
       break;
}
if(St.empty())
   t = -1;
else
   t = St.top();
//Calculating Li
area[i] = i - t - 1;
St.push(i);
}

//clearing stack for finding Ri
while (!St.empty())
St.pop();

for (i=len-1; i>=0; i--)
{
while (!St.empty())
{
   if(arr[i] <= arr[St.top()])
   {
       St.pop();
   }
   else
       break;
}
if(St.empty())
   t = len;
else
   t = St.top();
//calculating Ri, after this step area[i] = Li + Ri
area[i] += t - i -1;
St.push(i);
}

int max = 0;
//Calculating Area[i] and find max Area
for (i=0; i<len; i++)
{
area[i] = arr[i] * (area[i] + 1);
if (area[i] > max)
   max = area[i];
}

return max;
}

Complexity: 4 steps:
1) Finding Li = O(n)
2) Finding Ri = O(n)
3) Calculating Ai = O(n)
4) Finding max A(i) = O(n)

So Final complexity is O(n) + O(n) + O(n) + O(n) = O(n)

Subscribe - To get an automatic feed of all future posts subscribe here, or to receive them via email go here and enter your email address in the box. You can also like us on facebook and follow me on Twitter @akashag1001.