Question: An n-ary tree is represented in a matrix form such that A[i,j] = 1 if j is the ancestor of i. Otherwise A[i,j] = 0. Given this construct the tree.
(Question 2 from 2nd F2F in Amazon)

Example: Lets start with an example. If we have a tree like this:
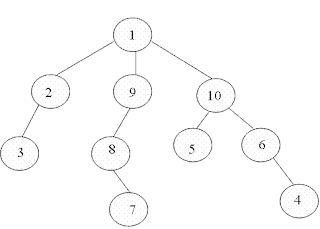
then its matrix will be something like this:


1

2

3

4

5

6

7

8

9

10

1











2

1










3

1

1









4

1





1




1

5

1









1

6

1









1

7

1







1

1


8

1








1


9

1










10

1











Answer: Firstly, we need to count ancestors for each of the nodes. So, we add a new column in the table, which will tell us the number of ancestor count for each node. And our new table will look like this:


1

2

3

4

5

6

7

8

9

10

no of anc

1











0

2

1










1

3

1

1









2

4

1





1




1

3

5

1









1

2

6

1









1

2

7

1







1

1


3

8

1








1


2

9

1










1

10

1










1

Now, we can clearly see from this table that '1' has no ancestor, so it must be the root node. So our initial tree will look like this:
And it is also clear that which the nodes has only one ancestor left they can be added in the partial tree constructed till now by seeing that whose child they are. For example ancestor count for '2' is 1 and in 2's row we can see that '1' is it's only ancestor left so we can add '2' as direct child to '1'. Same can be done with '9' and '10'. Now since all the direct child of 1 has been calculated we can set the 1's column as 'nil' and reconstruct ancestor count column. Now the new matrix and partial tree will look like this:


1

2

3

4

5

6

7

8

9

10

no of anc

1











0

2

nil










0

3

nil

1









1

4

nil





1




1

2

5

nil









1

1

6

nil









1

1

7

nil







1

1


2

8

nil








1


1

9

nil










0

10

nil










0
The same exercise can be repeated by seeing who all nodes has ancestor count as 1. Nodes '3', '5', '6' and '8' can be added to the partial tree and their parent columns can be removed. Now the new matrix and partial tree will look like this:


1

2

3

4

5

6

7

8

9

10

no of anc

1











0

2

nil










0

3

nil

nil









0

4

nil





1




nil

1

5

nil









nil

0

6

nil









nil

0

7

nil







1

nil


1

8

nil








nil


0

9

nil










0

10

nil










0

Again the same exercise can be repeated by seeing who all nodes has ancestor count as 1. Nodes '4' and '7' can be added to the partial tree and their parent columns can be removed. Now the new matrix and partial tree will look like this:


1

2

3

4

5

6

7

8

9

10

no of anc

1











0

2

nil










0

3

nil

nil









0

4

nil





nil




nil

0

5

nil









nil

0

6

nil









nil

0

7

nil







nil

nil


0

8

nil








nil


0

9

nil










0

10

nil










0

Now, we can see that ancestor count becomes 0 for all the nodes. So we can say that now the tree is complete and this is the answer.

Complexity of this exercise is left to the readers. I hope that I'm clear and the solution can be understood easily. I am also leaving the coding part to readers.

Subscribe - To get an automatic feed of all future posts subscribe here, or to receive them via email go here and enter your email address in the box. You can also like us on facebook and follow me on Twitter @akashag1001.